DeepLearing

1.引言

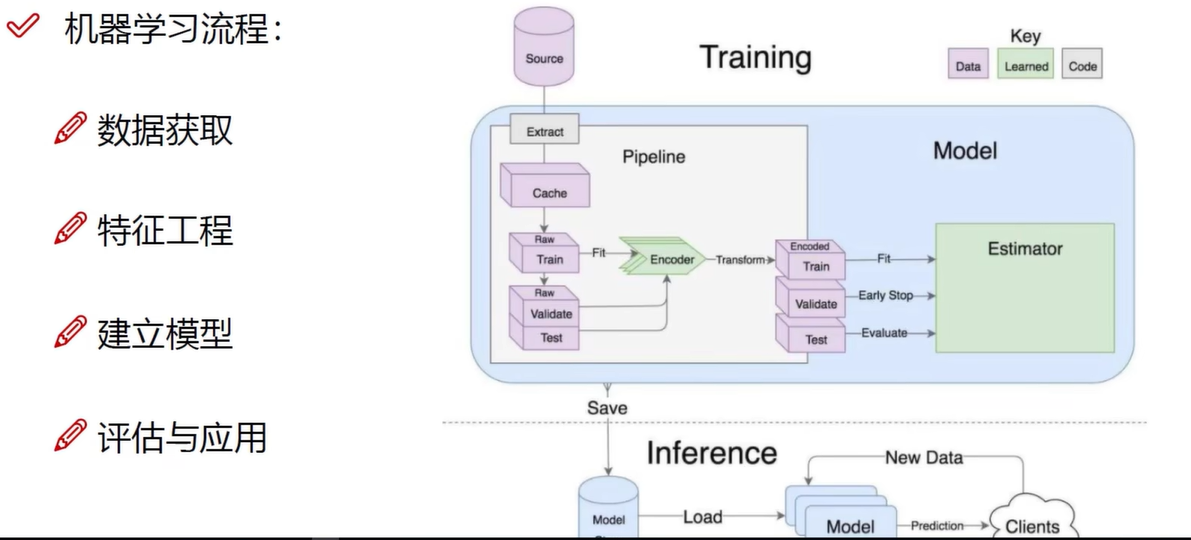
特征工程的作用：
- 数据特征决定了模型的上限
- 预处理和特征提取是最核心的
- 算法与参数选择决定了如何逼近这个上限

1.1反向传播

1.2正则化

1.3神经元

1.4激活函数

引入非线性特性，从而逼近任何分布结果。

激活函数对比：

Relu 为为主流，Sigmoid 会出现梯度消失现象

1.5数据预处理

不同的预处理结果会使得模型的效果发生很大的差异！

1. 参数初始化

• 参数初始化同样非常重要！
• 通常我们都使用随机策略来进行参数初始化
  $$W = 0.01*np.random.randn (D, H)$$

1.6Drop-Out

过拟合是神经网络非常头疼的一个大问题！

1.7卷积

计算过程如下图所示：

• 分别计算三个通道输入与卷积核进行内积，再将三通道结果求和得到输出（特征图）

特征图的个数（深度）等于卷积核的个数，如上图所见两个卷积核进行多尺度特征提取得到两个特征图。

1.7.1步长

步长就是卷积时滑动窗口的距离，一般为 1/2.

1.7.2边缘填充

边缘填充是在原输入的数据上加上一层 0 填充，不仅增加了原始边缘数据的卷积次数还保证了 0 填充填充不影响特征提取。

1.7.3卷积计算结果

长度：$$H_{2}= \frac{H_{1}-F_{H}+2P}{S}+1$$
宽度： $$W_{2}= \frac{W_{1}-F_{W}+2P}{S}+1$$

其中 W 1、H 1 表示输入的宽度、长度；W 2、H 2 表示输出特征图的宽度、长度；F 表示卷积核长和宽的大小；S 表示滑动窗口的步长; P 表示边界填充 (加几圈 0)。

1.8池化

最大池化

在原始特征图上分块选择最大（最重要）的特征值，从而对特征图进行下采样压缩大小，但特征图个数不变

1.9总体架构

只有带参数的才能称之为一层，卷积层和全连接层属于，而激活函数和池化层不属于。

特征图变化：

1.10感受野

卷积后的特征图中的特征值能够感受到的从原始输入数据的大小

[!NOTE] Problem

• P:如果堆叠 3 个 3*3 的卷积层，并且保持滑动窗口步长为 1，其感受野就是 7*7 的,
  这跟一个使用 7*7 卷积核的结果是一样的，那为什么非要堆叠 3 个小卷积呢？
• A: