Dateframe—Algorithm

本文最后更新于：1 年前

1.线性表

无论哪种数据结构，都存在增删改查 (按值查找)查（按位查找）操作，对应不同操作的时间复杂度不同，要根据实际数据的形式选择合适的数据结构进行存储，再选择合适算法进行处理。

顺序表（sequence list）

1初始化

2增加元素

3删除元素

4修改元素

5查找元素

按值查找

按位查找

1初始化

2增加元素

头插

尾插

3删除元素

4修改元素

5查找元素

按值查找

按位查找

2.栈

栈是一种后进先出（LIFO）的线性表结构。

顺序栈：

1
2
3
typedef struct {SElemType *base;
				SElemType *top;
				int stacksize;} SgStack;

链栈：

1
2
3
4
typedef struct StackNode{
SElemType data;
struct StackNode *next;}StackNode,*LinkStack;

1初始化

顺序栈：

1
2
3
4
5
6
7
Status InitStack(SgStack &S,int MAXSIZE{
S.base =new SElemType [MAXSIZE]；
if(!S.base） 
   return OVERFLOW;
   S.top = S.base;
   S.stacksize = MAXSIZE；
   return OK;

链栈：

不带头节点：

1
2
3
4
5
void Initstack (LinkStack &S)
{
	S=NULL;
}

2 入栈

顺序栈：
时间复杂度：O（1）

1
2
3
4
5
6
7

Status Push(SqStack &S,SElemType e)
{
if(S.top - S.base==S.stacksize）return ERROR;
*S.top++=e;
return OK;
}

这段代码是一个名为 Push 的函数，它接受两个参数：一个指向栈 S 的指针引用和要入栈的元素 e。SqStack 表示栈的类型，在这里推测它是由结构体或类定义的。&S 表示将栈变量的地址传递给函数，通过引用来修改栈的内容。在 C/C++中，引用有时候也被称为别名(alias)，它允许我们使用类似于指针的语法来操作对象，但是具有更好的安全性和易读性。SElemType 是栈元素的数据类型，可以是任何合法的数据类型。

这个函数的作用是将元素e压入到栈S中，如果栈已满则返回ERROR，否则在栈顶插入元素e并返回OK。其中S.top - S.base 表示当前栈中已有元素的个数，如果这个值等于S.stacksize就意味着栈已经满了。*S.top++=e表示将元素e存储在栈顶，并将栈指针往上移动一位，准备接收下一个元素。最后，函数返回插入操作的结果，OK表示成功，ERROR表示失败。

链栈：
头插

1
2
3
4
5
6
7
8
Status Push (LinkStack&S,ElemType e){
p=new StackNode;//生成新结点p
if (!p)return OVERFLOW;
p->data=e;
p->next=S;
S=p;//S始终指向当前第一个节点(栈顶节点)
return OK;

3 出栈

顺序栈：

1
2
3
4
5
6
7
Status Pop(SqStack &S,SElemType &e)
{
if(S.top == S.base）return ERROR;
e=*--S.top;
return OK;
}

链栈：

1
2
3
4
5
6
7
8
9
10
11
Status Pop (LinkStack &S,SElemType &e)
{
	if (S==NULL)
		return ERROR;
	e = S->data;
	p = S;
	S = S->next;
	delete p;
	return OK;
}

3. 队列

队列是一种先进先出（FIFO）的线性表，只允许在表的一端插入，另一端删除。

顺序队列：

1
2
3
4
5
6
Typedef struct {
QElemType *base;//初始化的动态分配存储空间
int front;//头指针
int rear;//尾指针
}SgQueue;

链队列：

1
2
3
4
5
6
7
8
9
10
11
typedef struct QNode
{
	QElemType data;
	struct Qnode *next;
}Qnode,*QueuePtr;
typedef struct 
{
	QueuePtr front;//队头指针
	QueuePtr rear;//队尾指针
}LinkQueue;

1 初始化

顺序队列：

1
2
3
4
5
6
7
8
9
Status InitQueue (SgQueue &Q)
{
Q.base = new QElemType[MAXQSIZE];
if (!Q.base)
	exit (OVERFLOW);
Q.front=Q.rear=0;
return OK;
}

链队列：
有头节点

1
2
3
4
5
6
7
8
9
Status InitQueue (LinkQueue &Q){
Q.front=(QueuePtr)malloc(sizeof(QNode));
if(!Q.front)
exit(OVERFLOW);
Q.rear=Q.front;
Q.front->next=NULL;
return OK;
}

队空标志：front==rear
队满标志：（rear+1）%M=front（循环队列）

2 入队

链接新节点，更新队尾节点

顺序队列：

1
2
3
4
5
6
7
8
Status EnQueue(SqQueue &Q,QElemType e)
{	if((Q.rear+1)%MAXQSIZE==Q.front)
		return ERROR;
	Q.base[Q.rear]=e;
	Q.rear=(Q.rear+1)%MAXQSIZE;
	return OK;
}

链队列：

1
2
3
4
5
6
7
8
9
10
Status EnQueue (LinkQueue &Q,QElemType e){
p=(QueuePtr)malloc(sizeof (QNode));
if(!p)
	exit(OVERFLOW);
p->data=e;
p->next=NULL;
Q.rear->next=p;
Q.rear=p;
return OK;
}

3 出队

临时存储首元节点，队头节点指向首元节点的下一个节点，删除释放首元节点

顺序队列：

1
2
3
4
5
6
7
8
Status DeQueue (LinkQueue &Q,QElemType &e)
{
if(Q.front==Q.rear)
	return ERROR;
e=Q.base[Q.front];
Q.front=(Q.front+1)%MAXQSIZE;
return OK;
}

链队列：

1
2
3
4
5
6
7
8
9
10
11
Status DeQueue (LinkQueue &Q,QElemType &e{
if(Q.front==Q.rear)
	return ERROR;
p=Q.front->next;
e=p->data;
Q.front->next=p->next;
if(Q.rear==p)
	Q.rear=Q.front;
free(p);
return OK;
}

最后一个节点的时候，不删除，要让队头等于队尾节点。

4 取队列长度

顺序队列：

1
2
3
4
5
int QueueLength(SqQueue Q)
{
	return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;
}

4. 串、数组和广义表

串就是字符串
数组包括一维数组和二维数组
广义表类似于 python 中的列表，可以表嵌套

5. 树

n 个节点的有限集合

1性质

  • 具有 n 个节点的完全二叉树的深度为
    $$log_2 n+1$$

两类特殊的二叉树：

  1. 满二叉树：指深度为 k 且含有 $2^k-1$ 个节点的二叉树。
  2. 完全二叉树：书中所含的 n 个节点和满二叉树中编号为 1 至 n 的节点一一对应。

2存储结构

顺序存储：

1
2
3
#define IMAXSIZE 100
typedef TElemType SqBiTree[MAXSIZE];
SqBiTree bt;

链式存储：

1
2
3
4
typedef struct{
   TEIemType data;
   struct BiTNode *Ichild, *rchild;
}BiTNode, *BiTree;

3遍历方式

先中后的顺序指的是根据点访问的顺序，如先序遍历就是根左右，后序遍历就是左右根。

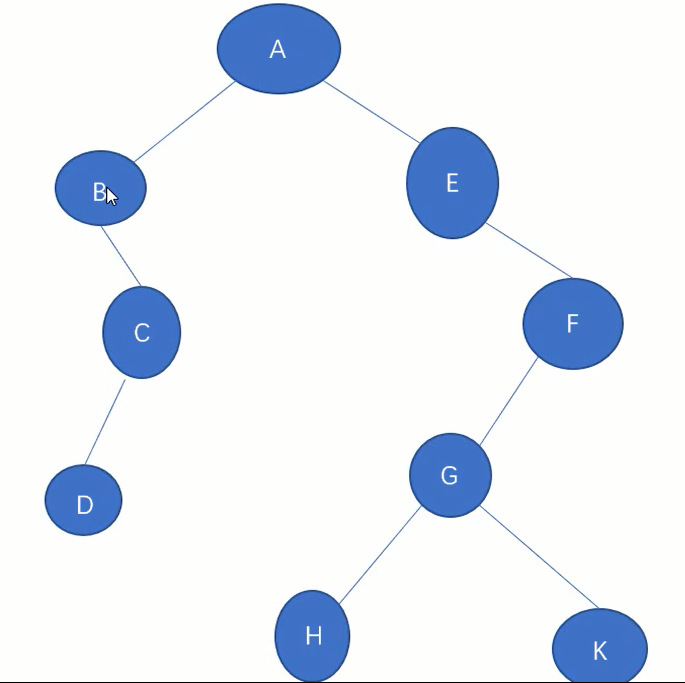
遍历图|275

先序遍历

ABCDEFGHK

1
2
3
4
5
6
7
8
void Preorder (BiTree T)
{
   if (T){
      visit(T->data);
      Preorder(T->IchiId);
      Preorder(T->rchiId);
   }
}

中序遍历

BDCAEHGKF

1
2
3
4
5
6
7
8
void Inorder (BiTree T)
{
   if (T) {
      Inorder(T->lchiId);
      visit(T->data);
      Ineorder(T->rchiId);
   }
}

中序非递归：

1
2
3
4
5
6
7
8
9
10
void Inorder1 (BiTree T)
{ 
Initstack(S); p=T;
while(1) {
while(p) {Push(S,p);p=p->lchild;}//先将左孩子全部入栈
if(StackEmpty(S)) return;
Pop(S,p);//出一个左孩子
cout<<P->data;
p=p->rchild;}
}

后序遍历

DCBHKGFEA

1
2
3
4
5
6
7
8
void bkorder (BiTree T)
{
   if (T) {
      bkorder(T->lchiId);
      bkorder(T->rchiId);
      visit(T->data);
   }
}

层次遍历

ABECFDGHK

4 常见应用

  1. 统计二叉树中叶子节点的个数：
1
2
3
4
5
6
7
8
9
void CountLeaf (BiTree T, int & count) {
	if(T){
		if(!T->lchild&&!T->rchild)
			count++;
		CountLeaf(T->lchild, count);
		CountLeaf(T->rchild, count);
	}
}

  1. 求二叉树的深度：
1
2
3
4
5
6
7
8
9
int Depth (BiTree I){
 if (!T) depthval = O;
 else {
    depthL= Depth(T->IchiId);//求左子树的深度
    depthR= Depth(T->rchild);//求右子树的深度
    depthval=1+ (depthL>depthR?depthL:depthR);//取较大者相加
   }
 return depthval;
}
  1. 建立二叉树的存储结构：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void CreateBiTree(BiTree &T){
	char ch;
	scanf("%c",&ch);
	if(ch="")
		T=NULL;
	else
		{
			T = new BiTNode;
			T->data = ch;
			CreteBiTree(T->lchild);//创建左子树
			CreteBiTree(T->rchild);//创建右子树
		}
}

  1. 查询二叉树中的某个节点：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool Preorder (BiTree T, ElemType x, BiTree &p){
if(T){
    if(T->data==x)//递归终止条件
	    { 
		    p = T;
		    return TRUE;
		}
	elseif{ 
		if(Preorder(T->lchild, x, p))
			return TRUE;
	elseif{
		if(Preorder(T->rchild, x, p))
			return TRUE;
	else{
			p = NULL;
			return False;
		}
	}
return False;
  1. 线索二叉树：

在中序线索二叉树中，查找结点*p的中序后继结点
1. 若 P->Rtag 为 1, 则 P 的右线索指向其后继结点q;
2. 若 P->Rtag 为 0, 则其后继结点q 是右子树中的最左结点。

  1. 森林于树之间的转换

左孩子右兄弟连接原则：左子树均为孩子节点，右子树均为兄弟节点。

  1. 哈夫曼树，降序排列，从低到高，两两（多多）做兄弟构造新树，循环往复
    所有叶子节点带权长度之和：
    $$
    WPL(T)=\sum W_kl_k(对所有叶子节点)
    $$

    WPL 最小的哈夫曼树为最优哈夫曼树。
    哈夫曼编码原则：左 0 右 1 原则

6. 图

7.

算法学习
#Dataframe-Algorithm
Dateframe—Algorithm
https://alleyf.github.io/2023/03/2e76a383274a.html
作者
alleyf
发布于
2023年3月17日
更新于
2023年5月24日
许可协议