FIR and IIR filter design

FIR和IIR滤波器设计与实现

一、要求

在子作业4的基础上，采用MATLAB的filterDesigner或fdatool工具箱，设计出相应的IIR滤波器和FIR滤波器。

二、实现思路

1.IIR滤波器设计实现

根据作业四得到的性能指标，利用MATLAB滤波器工具箱，输入性能指标参数选择效果最好的IIR滤波器进行滤波。

2.FIR滤波器设计实现

根据作业四得到的性能指标，利用MATLAB滤波器工具箱，输入截止频率**$f_c$**选择合适的窗函数设计得到FIR滤波器。

三、实现过程

1.性能指标分析

数字滤波器的频率响应表示为：
$$
H(e^{j\omega})=|H(e^{j\omega})|e^{j\beta(j\omega)}
$$
根据下图中理想低通滤波器逼近的误差容限可以看出，频率响应有通带、过渡带、阻带三个范围:

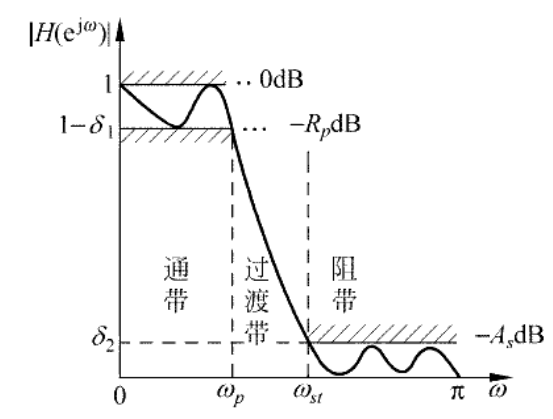
下图展示了不同滤波器的技术指标：

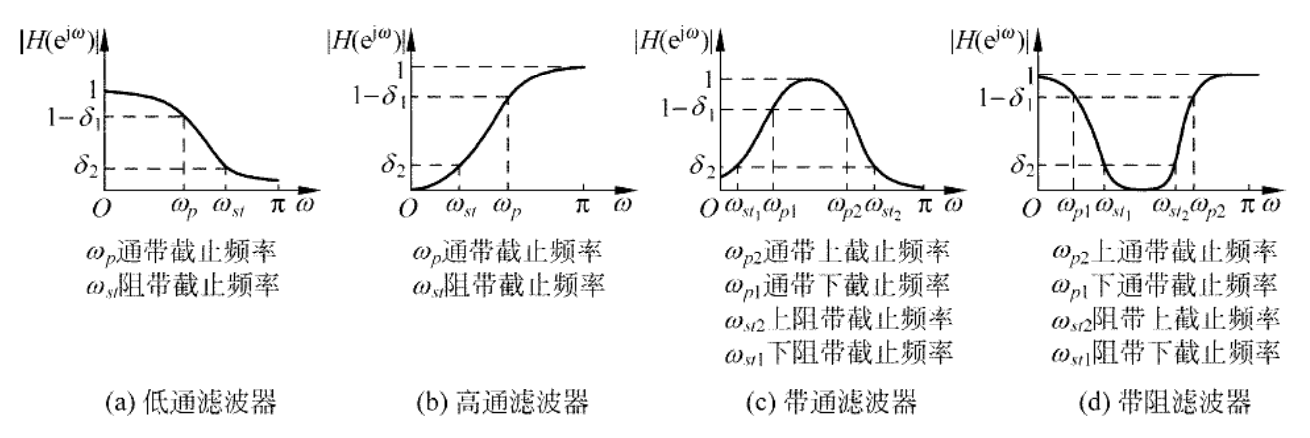
依据作业四得到的性能指标，通带截止频率**$w_p=10.7khz$，阻带截止频率$w_{st}=11.15khz$,通带最大衰减系数$\delta_1=2db$，阻带最小衰减$\delta_2=80db$**。可以使用MATLAB滤波器工具箱进行IIR和FIR滤波器的设计。

2.IIR滤波器设计实现

采用MATLAB的滤波器设计工具进行设计，在尝试不同种类的滤波器后，对比发现巴特沃斯滤波器的效果最佳，因此选择该滤波器来滤除噪声信号，设计得到的IIR滤波器结果如下图所示：

IIR滤波过程代码如下：

clc
clear all
%% 数据导入及参数设置
[x,Fs]=audioread('D:\DSP实验报告\大作业报告\ch4andch5\myaudio_11.15k_11.95k.wav');
x=x(:,1);%选择左声道
N=length(x);
t=(0:N-1)/Fs;%时域范围
df=Fs/length(t); %计算谱线间隔
f=t*df;%频域范围
X=FFT(x,N,Fs,t);
X=fftshift(X);%将频谱翻转过来
f=(f*Fs-Fs/2)/1e3;%只显示正频谱
X=abs(X);
% 绘出时域图和幅频响应
figure;
subplot(221)
plot(t,x);
title("原信号音频时域图");
xlabel("t/s");
subplot(222)
plot(f(:,ceil(N/2):end),X(ceil(N/2):end,1),'c')
title("原信号音频幅频响应");
xlabel("f/Khz"); 
%% IIR-Butterworth低通滤波器滤除高频噪声
y=filter(IIR,x);
Y=FFT(y,N,Fs,t);
Y=fftshift(Y);
Y=abs(Y);
% 绘出滤波后的时域图和幅频响应
subplot(223)
plot(t,y,'b');
title("IIR滤波后信号音频时域图");
xlabel("t/s"); 
subplot(224)
plot(f(1,ceil(N/2):end),Y(ceil(N/2):end,1),'g')
title("IIR滤波后信号音频幅频响应");
xlabel("f/Khz"); 
%% 试听及保存
sound(y,Fs);
audiowrite('./IIRfilter.wav',y,Fs)

3.FIR滤波器设计实现

采用MATLAB的滤波器设计工具进行设计，在尝试不同种类的窗函数后，对比发现布莱克曼窗的效果最佳，因此选择该窗函数来滤除噪声信号，设计得到的FIR滤波器结果如下图所示：

FIR时域和频域特性图如下图上所示：

FIR滤波过程代码如下：

clc
clear all
%% 数据导入及参数设置
[x,Fs]=audioread('D:\DSP实验报告\大作业报告\ch4andch5\myaudio_11.15k_11.95k.wav');
x=x(:,1);%选择左声道
Nx=length(x);
tx=(0:Nx-1)/Fs;%时域范围
df=Fs/length(tx); %计算谱线间隔
fx=tx*df;%频域范围
X=FFT(x,Nx,Fs,tx);%快速傅里叶变换
fx=(fx*Fs)/1e3;%只显示正频谱
X=abs(X);
% 绘出时域图和幅频响应
figure;
subplot(221)
plot(tx,x); 
title("原信号音频时域图");
xlabel("t/s"); 
subplot(222)
plot(fx(1,1:ceil(Nx/2)),X(1:ceil(Nx/2),1),'b')
title("原信号音频幅频响应");
xlabel("f/Khz"); 
%% blackman窗低通滤波器滤除高频噪声
y=filter(FIR,x);
Ny=length(y);%滤波后信号的长度
ty=(0:Ny-1)/Fs;%时域范围
Y=FFT(y,Ny,Fs,ty);%快速傅里叶变换求频谱
df=Fs/length(ty); %计算谱线间隔
fy=ty*df;%频域范围
fy=(fy*Fs)/1e3;%只显示正频谱
Y=abs(Y);
% 绘出滤波后的时域图和幅频响应
subplot(223)
plot(ty,y,"b");
title("FIR滤波后信号音频时域图");
xlabel("t/s"); 
subplot(224)
stem(fx(1,1:ceil(Ny/2)),Y(1:ceil(Ny/2),1),'c','.')
title("FIR滤波后信号音频幅频响应");
xlabel("f/Khz"); 
%% 试听及保存
sound(y,Fs);
audiowrite('./FIRfilter.wav',y,Fs)

四、结果展示

加噪信号经过IIR滤波器和FIR滤波器前后时域、频域对比图如下图所示：

由图可知IIR和FIR滤波器都很好的滤除了噪声信号，达到了预期的设计，IIR和FIR滤波后的音频依附录可见。

五、结果分析

1. IIR滤波器和FIR滤波器各自有各自的优缺点，都有不同的结构和实现方法。IIR滤波器结构简单容易实现，但是一般阶数较高，而且不稳定，相频响应不是完全线性相位。FIR滤波器一般阶数较低，相频响应具有完全的线性相位，系统绝对稳定，但是线性相位结构的FIR滤波器结构相对比较复杂难以实现。
2. IIR和FIR滤波器实际人工设计实现起来相对比较复杂，我们可以利用MATLAB中的滤波器设计工具箱辅助我们完成满足要求的各种滤波器，实现起来比较简单容易，

六、源码开源

源代码资源包有需要的小伙伴可以下载参考。