Frequency——Analysis

频谱分析及滤波指标设计

一、要求

为了完成对子作业1中音频信号的滤波，对子作业1中的音频信号进行频谱分析，并获取滤波器设计所需要的性能指标。

二、实现思路

1.频谱分析

1.读取音频

• 利用MATLAB的audioread函数读取原始音频（无噪声原始音频），该函数读取音频的实质是对音频进行采样，采样频率根据原始信号的情况而定。

2.FFT变换

• 对读取到的音频取单声道根据读取音频时得到的采样频率和频谱分辨率要求计算捕获时间和频谱间隔，进行进行FFT快速傅里叶变换得到原始音频信号的频谱，分析频谱的分布。

3.信号加噪

• 给原始信号加入高频带限噪声，加入噪声的频率范围为11.15khz~11.95khz。

4.FFT变换

• 对加噪后的音频信号进行FFT快速傅里叶变换，观察频谱的频率分布和范围。

5.失真分析

• 分析原始信号经过采样后的频谱是否存在频谱混叠和栅栏效应，如果有则改进加以去除。

2.设计性能指标

• 根据前面的频谱得到通带截止频率**$w_p$和阻带截止频率$w_s$**。

• 根据频谱设置通带容限**$\alpha1$和阻带容限$\alpha2$，进而得到通带最大衰减系数$\delta_1$和阻带最小衰减系数$\delta_2$**.

三、实现过程

1.读取原始音频信号及频谱分析

在MATLAB中利用audioread函数读取原始音频信号，并且绘出其时域图和频谱图，结果如下图所示。

由图可知原始音频信号的频谱从0~10.7khz左右就基本没有了，因此原始信号的最高频率**$f_{max}=10.7khz$**.

其源代码如下所示：

%% 数据导入及参数设置
[x,Fs]=audioread('D:\DSP实验报告\大作业报告\ch4andch5\myaudio.mp3');
x=x(:,1);%选择左声道
N=length(x);
t=(0:N-1)/Fs;%时域范围
df=Fs/length(t); %计算谱线间隔
f=t*df;%频域范围
X=FFT(x,N,Fs,t);
X=fftshift(X);%将频谱翻转过来
f=(f*Fs-Fs/2)/1e3;%只显示正频谱
X=abs(X);
% 绘出时域图和幅频响应
figure;
subplot(221)
plot(t,x);
title("原信号音频时域图");
ylabel('幅值');
xlabel("t/s");
subplot(222)
plot(f(:,ceil(N/2):end),X(ceil(N/2):end,1),'c')
% plot(f*Fs/1e3,Y,'k');
title("原信号音频幅频响应");
xlabel("f/Khz"); 
ylabel('频率幅值');

2.信号加噪及频谱分析

给原始音频信号加入频谱范围为11.15~11.95khz的高频带限噪声为后面设计滤波器做准备，绘出加噪信号的时域图和频谱图，如下图所示。

由上图观察可知加噪后的信号在11.15~11.95khz的范围内出现了高频噪声信号，这也是后面需要滤波消除的部分，根据加噪后的信号的频谱可以得到设计滤波器的性能指标。

源代码如下所示：

%% 加入噪声
noise=0;
for i=0.1:0.1:5
    noise=noise+0.003*(cos((70+i)*1000*t));
end
x_z=x+noise';
X_Z=FFT(x_z,N,Fs,t);
X_Z=fftshift(X_Z);%将频谱翻转过来
X_Z=abs(X_Z);
subplot(211)
plot(t,x_z);
xlabel("t/s");
ylabel('幅值');
title('加噪后信号时域图');
subplot(212)
plot(f(:,ceil(N/2):end),X_Z(ceil(N/2):end,1),'c')
xlabel('f/Hz');
ylabel('频率幅值');
title('加噪后信号幅频响应');

3.失真分析

由上述的频谱图可知原始音频信号**$f_{max}=10.7khz<f_s=48khz$**,因此经过采样后信号没有发生频谱混叠，且没有栅栏效应发生。

4.设计性能指标

数字滤波器的频率响应表示为：
$$
H(e^{j\omega})=|H(e^{j\omega})|e^{j\beta(j\omega)}
$$
根据下图中理想低通滤波器逼近的误差容限可以看出，频率响应有通带、过渡带、阻带三个范围:

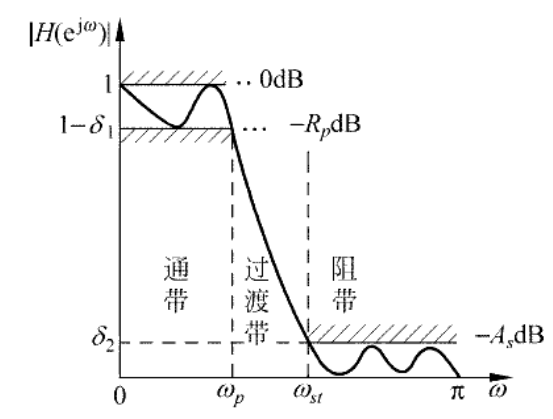
下图展示了不同滤波器的技术指标：

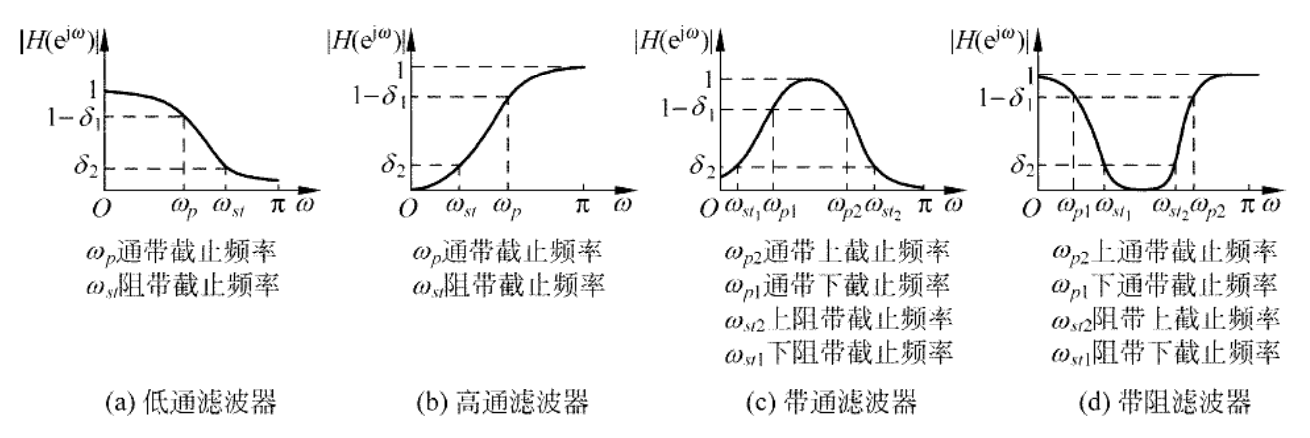
对加噪后的音频频谱进行分析，有用信号的频谱范围是0~10.7khz，噪声信号的频谱范围是11.15~11.95khz，因此设置通带截止频率**$w_p=10.7khz$，阻带截止频率$w_{st}=11.15khz$,通带最大衰减系数$\delta_1=2db$，阻带最小衰减$\delta_2=80db$**。

四、结果展示

原始音频信号加噪前后时域、频域对比图如下图所示：

设计滤波器的性能指标如下：

通带截止频率**$w_p=10.7khz$，阻带截止频率$w_{st}=11.15khz$,通带最大衰减系数$\delta_1=2db$，阻带最小衰减$\delta_2=80db$**。

五、结果分析

1. 谱分析的过程中首先要知道分辨率和采样频率等要求，然后根据原始信号的最大频率结合奈奎斯特采样定理设定合适的采样频率，再依据$F_0=\frac{1}{T_0}=\frac{1}{N*T_s}$计算得到采样点数和捕获时间等信息，计算频域窗口范围，接着进行FFT变换获得其频谱，观察频谱与理论频谱是否一致，判断是否发生频谱混叠、栅栏效应等，若使用了窗函数进行截断还要考虑是否发生频谱泄露。
2. 设计滤波器性能指标过程中，首先需要知道待滤波信号的频谱情况，然后依据频谱判断有用信号和噪声信号的分布，从而确定使用低通、高通、带通还是带阻等滤波器，并且设计相应的性能指标，一般包括通带截止频率、阻带截止频率、通带最大衰减和阻带最大衰减四个性能指标。

六、源码开源

源代码资源包有需要的小伙伴可以下载参考。