本文最后更新于：6 个月前

信号的时域处理

一、要求

选择子作业１中的音频信号，自行给定滤波器的系统函数，分别采用时域线性卷积和差分方程两种方法对音频信号进行滤波处理，比较滤波前后信号的波形和回放的效果。

二、实现思路

1.时域卷积法

分析原始音频信号的频谱，观察有用信号和噪声的分布，选择滤波器类型（低通、高通、带通、带阻等）
设定幅频响应下降三分贝的截止频率和滤波器阶数
选择合适的窗函数（包括Rectangular、Hanning、Hamming、Bartlett、Blackman、Kaiser、Gaussian、Flat-top等）
计算滤波器系数（滤波器的单位脉冲响应）
将滤波器系数与原始信号卷积进行滤波

2.差分方程法

分析原始音频信号的频谱，观察有用信号和噪声的分布，选择滤波器类型（低通、高通、带通、带阻等）
设置通带截止频率和阻带截止频率并归一化，设定通带纹波系数和阻带衰减系数
求出切比雪夫滤波器的阶数和下降3分贝通带截止频率
计算滤波器的差分方程系数
调用filter函数对原始信号进行滤波

三、实现过程

滤波前后对比图

FIR hamming窗低通滤波器前后对比图

IIR 切比雪夫低通滤波器前后对比图

1.时域卷积

首先导入原始音频信号并画出时域图和幅频响应曲线，分析其频谱分布，代码如下所示。

%% 数据导入及参数设置
[x,Fs]=audioread('D:\数据\Carmen_overture_noisy_8k_9.5k.wav');
Nx=length(x);
tx=(0:Nx-1)/Fs;%时域范围
df=Fs/length(tx); %计算谱线间隔
fx=tx*df;%频域范围
X=FFT(x,Nx,Fs,tx);%快速傅里叶变换
fx=(fx*Fs)/1e3;%只显示正频谱
X=abs(X);
% 绘出时域图和幅频响应
figure;
subplot(221)
plot(tx,x); 
title("原信号音频时域图");
xlabel("t/s"); 
subplot(222)
% plot(fx*Fs/1e3,abs(X),"blue")
plot(fx(1,1:ceil(Nx/2)),X(1:ceil(Nx/2),1),'b')
title("原信号音频相频响应");
xlabel("f/Khz");

观察其幅频响应发现有用信号的频率在8Khz以下，以上则为能量较大的高频噪声，因此我采用低通滤波器对其进行滤波。

FIR滤波器

设FIR滤波器的单位冲激响应h(n)为一个N点序列，0≤n≤N-1，则滤波器的系统函数为：
$$
H(\mathrm{z})=\sum_{k=0}^{N-1}h(\mathrm{k})*\mathrm{z}^{-k}
$$
直接型FIR滤波器的差分方程为：
$$
\mathrm{y(n)}=\sum_{m=0}^{N-1}\mathrm{h(m)x(n-m)}
$$
由差分方程可知只需要求出FIR滤波器的单位冲激响应h(n)，设置滤波阶数和3db通带截止频率fc，采用汉林窗函数处理，再使用fir1函数将其与待滤波信号卷积即可完成滤波，具体实现代码如下。

%% hamming窗低通滤波器滤除高频噪声
fc=7.95e3; %下降3分贝截止频率
h_n=fir1(1000,fc*2/Fs,"low");
y=conv(h_n,x);

Ny=length(y);%滤波后信号的长度
ty=(0:Ny-1)/Fs;%时域范围
Y=FFT(y,Ny,Fs,ty);%快速傅里叶变换求频谱
df=Fs/length(ty); %计算谱线间隔
fy=ty*df;%频域范围
fy=(fy*Fs)/1e3;%只显示正频谱
Y=abs(Y);
% 绘出滤波后的时域图和幅频响应
subplot(223)
plot(ty,y,"g");
title("滤波后信号音频时域图");
xlabel("t/s"); 
subplot(224)
stem(fx(1,1:ceil(Ny/2)),Y(1:ceil(Ny/2),1),'c','.')
title("滤波后信号音频相频响应");
xlabel("f/Khz"); 
%% 试听及保存
% sound(y,Fs);
audiowrite("D:\数据\FIRfilter.wav",y,Fs);
%% 快速傅里叶变换函数
function FourierTransform = FFT(signal,N,fs,t)
Y=fft(signal,N);
df=fs/length(t); %计算谱线间隔
f=t*df;%频域范围
Ys=abs(Y); %幅度响应
FourierTransform=Ys;
end

FIR滤波器的单位冲激响应如下图所示：

通过时域卷积得到滤波后的结果如下图所示：

由图可知，发现经过1000阶的3分贝截止频率为7.95e3Khz的低通滤波器处理后，8Khz及以上的高频噪声基本被完全滤除，成功从原始音频信号中提取到有用信号。

2.差分方程

首先也是先对原始音频信号做傅里叶变换分析其频谱，频谱结果同上，这里不在赘述。

IIR切比雪夫低通滤波

IIR(infinite impulse response)滤波器，无限冲激响应滤波器,IIR滤波器定义如下：
$$
\sum_{l=0}^{N}a(l)y(n-l)= \sum _{k=0}^{M}b(k)x(n-k)
$$
令$a(0)=1,a(l),l=1,2,…N$取反后得：
$$
y(n)= \sum _{k=0}^{M}b(k)x(n-k)+ \sum _{l=1}^{N}a(l)y(n-l)
$$
IIR直接II型滤波器的流程框图如下所示：

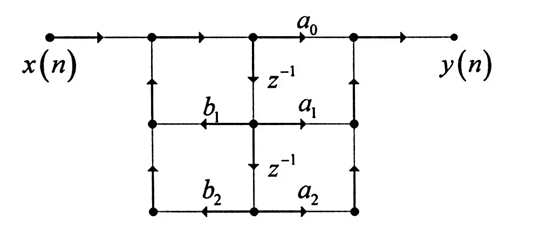
根据流程框图可知，需要求得差分方程系数向量a和b，这里我采用常见的切比雪夫滤波器设定通带频率、阻带频率以及纹波系数和衰减系数计算出系数a和b，再利用filter函数传入系数a、b和待滤波信号即可完成滤波，采用如下代码实现差分方程法实现IIR切比雪夫低通滤波器。

%% IIR-Chebyshev低通滤波器滤除高频噪声
Wp=7.6e3*2/Fs;%通带频率
Ws=8e3*2/Fs;%阻带频率
[n,Wc]=cheb1ord(Wp,Ws,2,40);%计算阶数和3db通带截止频率
[b,a]=cheby1(n,3,Wc);%切比雪夫滤波器返回差分方程系数
freqz(b,a);%绘出滤波器频谱图（幅频响应和相频响应）
y=filter(b,a,x);%滤除高频噪声
Y=FFT(y,N,Fs,t);
Y=fftshift(Y);
Y=abs(Y);
% 绘出滤波后的时域图和幅频响应
subplot(223)
plot(t,y,'b');
title("滤波后信号音频时域图");
xlabel("t/s"); 
subplot(224)
% plot(f*Fs/1e3,Y,'k');
plot(f(1,ceil(N/2):end),Y(ceil(N/2):end,1),'g')
title("滤波后信号音频幅频响应");
xlabel("f/Khz");

IIR切比雪夫滤波器的归一化频谱图如下所示：

观察发现其幅频响应滤波效果比较好，根据此滤波器对原始音频信号进行滤波，下图展示了滤波后的结果。

由图可知8Khz及以上的高频噪声被滤除，但原始信号靠近8Khz的部分幅值也有所衰减但影响不大，从而实现了对有用信号的提取。

四、结果分析

时域线性卷积法和差分方程法都是实现数字滤波的两种方法，都可以很好的滤除有用信号的噪声，从而提取出有用的信号，排除无用信号的干扰。
实际观察发现随着滤波器的阶数的升高，滤波器的频率响应越接近理想滤波器，而要想实现同样滤波效果，差分方程法的滤波器阶数远小于时域卷积法的阶数。
当使用IIR滤波器时，由于IIR滤波器的存在系统稳定性问题，因此当滤波器阶数过高时会导致系统不稳定，从而失去正常滤波能力。
将相同参数的IIR巴特沃斯滤波与切比雪夫滤波对比，发现切比雪夫滤波后残留噪声频谱分布均匀，而巴特沃斯滤波后残留噪声频谱频率与幅度成反比，但是两种滤波器对高频有用信号也都所衰减，说明难以实现理想滤波器，只能无限逼近，两者频谱对比图如下。