Chain-of-Thought Reasoning Without Prompting

无提示的思维链推理

手工构造 COT 提示 ✖️ 内在 COT 激发 ✔️

汇报人：范财胜
汇报时间：2024-04-19
联系方式：alleyf@qq.com

📕 目录

• 引言
• 研究方法
• 实验结果
• 研究结论
• 创新点
• 感想&疑问

📜 引言

Meta	Value
标题	Chain-of-Thought Reasoning Without Prompting
期刊/会议	arXiv 预印本
作者	Xuezhi Wang， Denny Zhou
来源	Google DeepMind：与 Google Brain（Transformer）同为 Google 的人工智能研究实验室，代表作 AlphaGo，WaveNet，AlphaFold 等，即将与 Google Brain 合并
日期	2024-02-15
原文链接	https://arxiv.org/pdf/2402.10200v1.pdf
标签	COT, 推理能力, 解码过程

1 📑 Background

在增强大语言模型（LLMs）的推理能力方面，先前的研究主要集中在特定的提示技术或指令微调上，例如少样本或零样本思维链（CoT）提示（包括改进提示、代理模型、控制和验证生成的步骤[逐步验证，过程反馈，波束搜索引导的自评估]、理解思想链的产生）。

增强 LLM 推理能力

• 要求显示某些中间步骤的具体指令的零样本提示
• 带有中间步骤增强演示范例的小样本提示
• 大量思想链 (CoT) 推理数据进行模型训练或指令微调

这些方法虽然有效，但往往需要大量的手动工程和特定任务的调整，限制了模型的泛化能力和应用范围。

• ==LLM 能否在没有提示的情况下有效地进行推理？==
• ==它能推理到什么程度？==

---

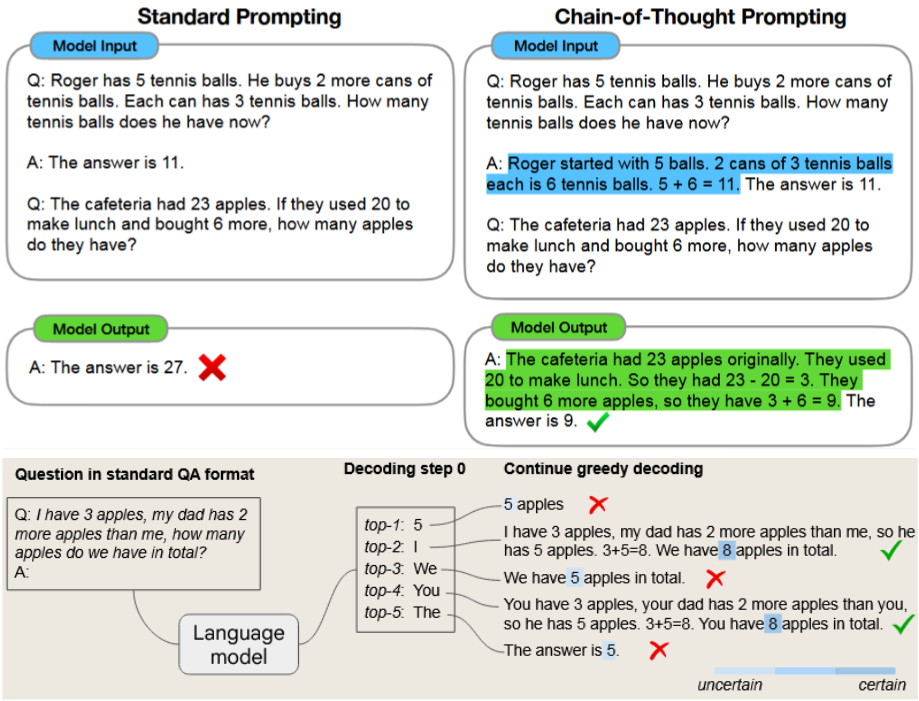
图 1标准提示、CoT 提示和CoT 解码对比图

2 ⚜ Motivation

探索并利用大语言模型内在推理路径，解放 COT 提示模板的手工构建。

• 探索 LLMs 的内在推理能力：在没有外部提示的情况下，LLMs 是否能够自然地生成推理路径，这有助于揭示模型的真实能力和潜力。
• 简化模型使用和优化过程：通过探索不依赖于特定提示的解码方法，可以简化模型的使用和优化过程，使其更易于迁移和扩展到不同的任务和领域。

3 👑 Contribution

• 提出 CoT-decoding 方法：文章提出了一种新的解码方法 CoT-decoding，它通过考虑解码过程中的顶部候选词来自然地生成推理路径。
• 评估模型的内在推理能力：CoT-decoding 方法允许研究者更准确地评估 LLMs 的内在推理能力，而无需依赖于外部提示。

📊 研究方法

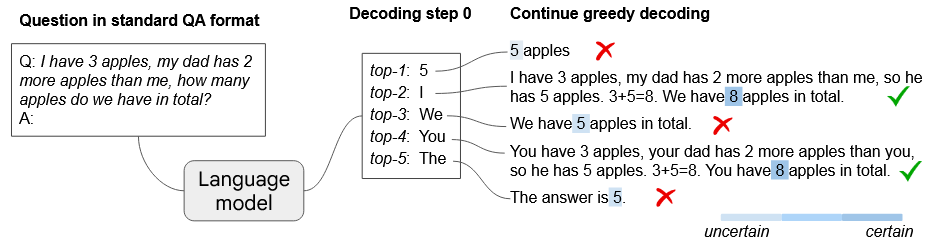
图 2 CoT 解码图

由图可知，预训练的 LLM 能够无需提示进行固有推理，而不是仅仅依赖于 top-1 ==贪婪解码==路径。此外，当存在 CoT 推理路径时，这些模型在解码最终答案（由较暗的阴影颜色表示）时往往表现出==更高的置信度==。
路径 2 和 4 在得出正确答案“8”时显示出更高的确定性，与导致错误答案“5”的路径中的高度不确定性形成鲜明对比。

1 分支引导

图 3 多分支跨任务的贪婪解码路径和替代 top-k 路径解码示例图

• 采用==贪婪解码==通常不包含 CoT 路径，而是直接解决问题，可能由于大量简单问题的预训练导致对问题难度的扭曲认知。
• 但是把解码的第一步作为分支，使用候选的 top-k 的 token，后续继续使用贪婪解码的方法，发现自发的生成了一些 ==Cot 路径==。

2 路径提取

既然存在模型本身固有 CoT 推理路径，那么该 如何提取该路径引导模型输出呢？
==现象：== 在模型的概率评估中，CoT 路径的排名并不总是高于非 CoT 路径。此外，它们往往不能代表所有路径中的主导答案。例如，在 GSM8K 问题中，普遍的答案“60”与贪婪解码结果一致，无法作为识别正确路径的可靠指标。
==方法：== 在检查模型的 logits（原始预测值）后，发现 CoT 路径的解码结果通常具有更有高的概率置信度，即 decode 每步中，概率最大的 token 和概率次大的 token 之间存在显著的概率差异：

$$
\Delta_{k,\text{answer}} = \frac 1 n \sum _ { x _ t \in \text{answer}} p ( x _ t ^ 1 \mid x _ { < t })-p(x_t^2\mid x_{<t})
$$

其中$x^1_t$ 和 $x^2_t$代表着在第 k 条路径的第 t 个解码步骤中排名最高的两个 token，$n$ 代表答案的 token 总数。这种基于最终答案对应 token 的概率置信度的方法称为CoT-Decoding。

另一种是根据解码路径的长度来选择 CoT 路径（直觉上，更长的解码路径更有可能包含 CoT）。这种基于长度的选择方法在一定程度上适用于数学推理问题，但在其他推理任务中的普适性是有限的。

3 分支选择

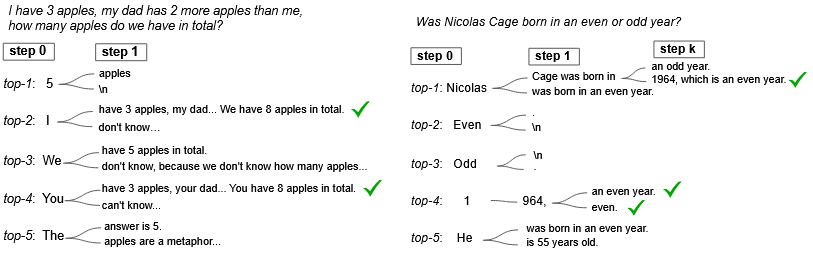
图 4 不同解码步骤中的替代 token 的分析

那么为什么选择解码的第一个步骤而不是其他阶段进行分支呢？
==现象：== 早期分支，例如在第一个解码步骤，显著增强了潜在路径的多样性。相反，后期分支会受到先前生成的令牌的显著影响。例如，以标记“5”启动会大大降低纠正错误路径的可能性。尽管如此，最佳分支点可能会因任务而异；例如，在年奇偶校验任务中，中路径分支可以有效地产生正确的 CoT 路径。
==思考：== 悬崖勒马，为时不晚！

4 路径聚合

由于考虑了 top k 解码路径，一种自然的扩展是聚合所有这些路径上的答案，类似于多数投票机制。这种聚合背后的基本原理是减轻对于模型 logits 中微小差异的敏感性。但是由于路径中大多数答案都是错误的，因此提出了一种加权聚合方法最大化$\tilde{\Delta}_{a}$：

$$\tilde{\Delta}{a}=\sum{k}\Delta_{k,a}$$

$\Delta_{k,a}$ 是答案为 a 的第 k 个解码路径的置信度，把答案相同的多个解码路径的置信度进行加权聚合，得分最高的答案作为最终答案，这种聚合增强了结果的稳定性。

🔬 实验结果

实验设置
对于所有实验，模型的默认输入是标准 QA 格式 ：

标准 QA 格式
Q: [question]
A:，
其中 [question] 根据任务填充实际问题，在解码过程中，使用 k = 10 作为第一个解码位置替代 top-k token 的默认值。

模型选择

• PaLM-2 预训练的模型系列，具有不同的尺度，范围从 X-Small、Small、Medium 到 Large；
• Mistral-7B 开源模型，实验主要集中在预训练模型上，但也包括指令调整模型（表示为“inst-tuned”或“IT”）的实验。

在一系列推理基准测试中评估了 CoT 解码方法，证明了其在解码过程中不需要专门的提示即可成功恢复 CoT 推理路径的能力。

1 K 值的选择

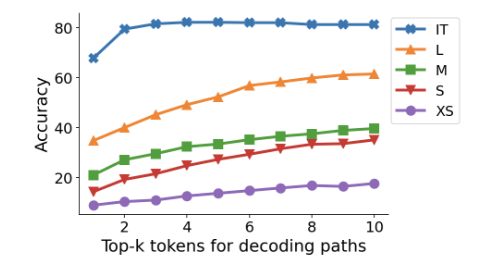
图 5 PaLM-2 模型系列的 GSM8K 数据集的准确性与解码中使用的 top-k token 的关系

• 较高的 k 值通常会提高模型性能，这表明在许多情况下，正确的 CoT 路径可能确实存在，但在模型解码过程中 通常排名较低。
• 对于指令调整模型，k 的影响不太显着，表明 指令调整过程有效地将大部分 CoT 路径引入到前几个解码路径。

2 数学推理任务

任务设定：小学数学问题（GSM8K）以及多步算术数据集。
表 1 不同大小的 PaLM-2 模型系列的数学推理任务的准确性

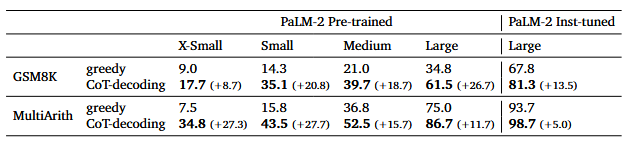
推理能力增强： 与贪婪解码方法相比，CoT 解码显著增强了模型的推理能力，并且在所有模型尺度上一致。例如，在 GSM8K 上，与 PaLM-2 Large 模型上的贪婪解码相比，CoT 解码的绝对精度提高了26.7%。此外，CoT 解码 缩小了预训练模型和指令调整模型之间的差距（例如，在大模型尺寸上），证明了使用足够的 CoT 数据进行 指令微调也可以通过修改预训练模型内的解码过程来部分实现。
微调模型优化： 在指令调优的微调过程中已经纳入了丰富的 CoT 注释。因此，模型在处理推理任务时有望固有地生成 CoT 路径。然而，在分析具体示例时，即使在指令微调后，模型偶尔也会坚持尝试直接解决问题。相比之下，CoT 解码可以通过 首先触发 CoT 来增强对替代路径的探索，从而导致更准确的问题解决。

3 自然语言推理任务

任务设定：出生年份奇偶校验（GPT-4 这样的 SOTA 模型也难以完成此类任务）。整理了一份前 100 位名人的名单，通过网络搜索手动提取并验证了他们的出生年份，以通过算法建立基本事实，根据真实情况（“偶数”或“奇数”）评估模型的响应，以计算此任务的最终准确性。
表 2 不同大小的 PaLM-2 预训练模型的年奇偶校验任务的准确性

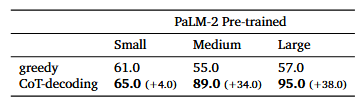
推理一致性： 贪婪解码的准确性即使是最大的模型也只是 57%， 而CoT 解码在多数情况下可以恢复 CoT 路径，并达到 90% 以上的准确率。误差分析表明，大多数误差源于模型检索到错误的出生年份，而生成的 CoT 路径在奇偶性和模型检索的年份之间保持高度一致。
阈值触发： 当模型尺寸较小时，即使给出了正确的年份，模型也无法确定奇偶性。因此，==对于小于等于“小”比例的模型尺寸，性能变化不大，即小模型因知识匮乏不足导致不具备内在 COT 推理能力。==

4 符号推理任务

任务设定：
（1）硬币翻转，有 2、3、4 轮的潜在翻转；以及来自 Big-Bench-Hard 的两项任务。
（2）谎言网络，包含 3、4、5 个真/谎言陈述。
（3）多步运算，不同的深度水平 d 和长度 l。
（4） 运动理解和对象计数，Big-Bench 的两个综合任务，探究模型解决综合任务的内在能力。
表 3 PaLM-2 预训练大型模型上符号推理任务和其他 Big-Bench 任务的准确性

复杂任务思维退化： 当任务复杂性增加且高度综合时（即任务在预训练分布中缺乏显着的表示时），模型无法生成准确的 CoT 路径，表明语言模型很大程度上受到它们所训练的数据分布的影响。

5 方法对比

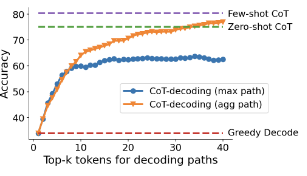
图 6 PaLM-2 Large 模型的 GSM8K 数据集上的 COT 和贪婪解码与少样本和零样本提示对比

• 与仅采用最大路径相比，聚合路径方法显著提高了准确性，表明它可以通过减轻对模型 logits 中微小差异的敏感性来稳定结果。
• 聚合路径产生类似于小样本 CoT 提示的性能，表明该任务上模型具有有效解决该任务的内在能力。
• few-shot CoT 提示可能有助于使模型的内在 CoT 路径更接近 top-1 路径。

---

• 与其他 CoT 提示方法相比，CoT 解码表现出更“自由形式”的 CoT 生成。这种分歧可能归因于两个因素：（1）作者鼓励初始解码步骤的多样性（2）缺乏提示所施加的明确约束。
• CoT 解码可以更好地 揭示LLMs解决问题的内在策略，而不受提示设计者可能产生偏见的外部提示的影响。观察到 few-shot CoT 路径很大程度上受到少样本提示的影响，始终遵循标准的分析方法——首先评估人的职业，然后评估该职业是否与行动相符。相反，CoT 解码揭示了偏离传统问题解决方法的路径，尽管在某些情况下根据基本事实产生了错误的最终答案，但 CoT 路径仍然有效。

6 模型迁移

作者还对其他模型系列进行了实验，特别是开源的 Mistral-7B 模型。评估预训练模型（“Mistral-7B-v0.1”）和指令调整变体（“Mistral-7B-Instruct-v0.1”）。
表 4 Mistral-7B 预训练和指令调整模型的推理性能

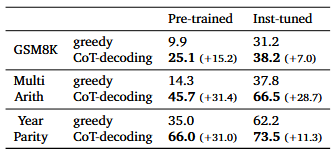
综上所述，CoT-Decoding 使得各个模型系列一致增强，涵盖数学推理（GSM8K 和 MultiArith）、自然语言推理（年份奇偶校验）和符号推理（硬币反转）等任务，显著改进了的贪婪解码。

🚩 研究结论

• 内在推理能力的揭示：CoT-decoding 方法能够揭示 LLMs 的内在推理能力，即使在没有外部提示的情况下，模型本质上也具有跨广泛任务集生成思维链推理路径的能力。
• 推理任务的改进：CoT 推理路径的存在与解码最终答案的模型置信度增加相关，CoT 解码从语言模型中提取更可靠的解码路径，从而提高整体推理性能，实现与小样本提示相当的效果，并且具备跨模型和任务的通用性。
• 复杂任务的局限性：内在 COT 推理路径在预训练数据中频繁表示的任务中更为普遍，而在复杂的综合任务中则较少，在这些任务中，可能仍然需要高级提示来触发这些推理路径。

📌 创新点

无提示推理增强：CoT-decoding 是一种不依赖于特定提示的无监督推理增强方法，能够检查模型生成 CoT 路径的内在能力，而不需要借助微调或任何额外的模型。

CoT 解码提供了一种无需明确提示即可从预先训练的 LLM 中获取推理能力的替代方法。此外，它绕过了提示引入的混杂因素，从而能够更准确地评估模型的内在推理能力。CoT 解码会在解码过程中自发地揭示 CoT 推理路径，从而显著增强模型在各种基准上相对于贪婪解码的推理能力。

💡 感想 & 疑问

• CoT-Decoding 对于复杂任务增益效果一般，如何进一步优化 CoT-Decoding 方法以适应更复杂的推理任务？
• CoT-Decoding 方法与传统的贪婪解码相比，在计算成本上是否有显著增加，这种代价是否值得，又该如何保持性能不变的同时降低计算开销？
• CoT-decoding 方法是否适用于除英语之外的其他语言？如果是，其跨语言的推理能力如何？

致谢

感谢各位老师和师兄师姐们的聆听，如有不当敬请批评指正！

后期目标：学习 pytorch 框架的使用，继续阅读基础经典论文与前沿价值论文。